递归实现
使用公式f[n]=f[n-1]+f[n-2],依次递归计算,递归结束条件是f[1]=1,f[2]=1。 需要注意频繁的函数调用对性能的影响。
int fib(int n)
{
if(n == 0)
return 0;
if(n == 1)
return 1;
if(n > 1)
return fib(n-1) + fib(n-2);
}
数组实现
空间复杂度和时间复杂度都是0(n),效率一般,比递归来得快。
int fib(int n)
{
if(n == 0)
return 0;
if(n == 1 || n == 2)
return 1;
int *a = new int[n+1];
a[0]=0;
a[1]=1;
for(int i=2; i <= n; i++)
{
a[i] = a[i-1] + a[i-2];
}
int m = a[n];
delete[] a;
return m;
}
迭代实现
迭代实现是最高效的,时间复杂度是0(n),空间复杂度是0(1)。
int fib(int n)
{
int x, y, z;
if(n == 0)
return 0;
else{
x = 0;
y = 1;
z = 0;
for(int i=1; i < n; i++)
{
z = x + y;
x = y;
y = z;
}
return y;
}
}
公式实现
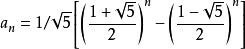
如图,通用公式又称为“比内公式”,是用无理数表示有理数的一个范例。
int fib(int n)
{
double gh5=sqrt((double)5);
return (pow((1+gh5),n)-pow((1-gh5),n))/(pow((double)2,n)*gh5);
}
二分矩阵实现
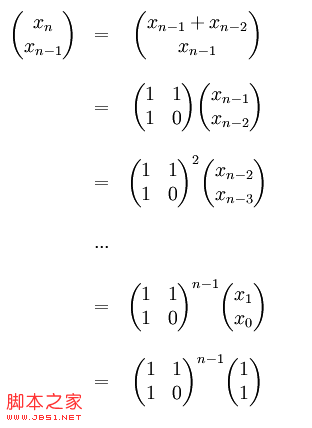
如图,Fibonacci 数列中任何一项可以用矩阵幂算出,而n次幂是可以在logn的时间内算出的。 下面贴出来的demo我没看懂,数学知识早忘记了, 囧tz
void multiply(int c[2][2],int a[2][2],int b[2][2],int mod)
{
int tmp[4];
tmp[0]=a[0][0]*b[0][0]+a[0][1]*b[1][0];
tmp[1]=a[0][0]*b[0][1]+a[0][1]*b[1][1];
tmp[2]=a[1][0]*b[0][0]+a[1][1]*b[1][0];
tmp[3]=a[1][0]*b[0][1]+a[1][1]*b[1][1];
c[0][0]=tmp[0]%mod;
c[0][1]=tmp[1]%mod;
c[1][0]=tmp[2]%mod;
c[1][1]=tmp[3]%mod;
}//计算矩阵乘法,c=a*b
int fibonacci(int n,int mod)//mod表示数字太大时需要模的数
{
if(n==0) return 0;
else if(n<=2) return 1;//这里表示第0项为0,第1,2项为1
int a[2][2]={ {1,1}, {1,0} };
int result[2][2]={ {1,0}, {0,1} };//初始化为单位矩阵
int s;
n-=2;
while(n>0)
{
if(n%2 == 1)
multiply(result,result,a,mod);
multiply(a,a,a,mod);
n /= 2;
}//二分法求矩阵幂
s=(result[0][0]+result[0][1])%mod;//结果
return s;
}

